Let us first look at the
so-called representative elements, Groups 1A-8A. How
do they usually form ions? The answer is realtively simple:
A-type elements are
"happiest" when they can achieve an inert gas configuration.
For instance, Na "likes" to lose a
single electron to achieve the same electron configuration as Neon.
That is,

On the other hand, F "likes" to
gain an electron to achieve the same electron configuration as Neon.
In this case,

The main point here is that
inert gas configurations are particularly stable!
In general, group 1A atoms lose
one electron to get down to the previous inert gas. That is,
|
Li loses one electron to
|
gain the [He] configuration.
|
|
Na loses one electron to
|
gain the [Ne] configuration.
|
|
K loses one electron to
|
gain the [Ar] configuration.
|
|
Rb loses one electron to
|
gain the [Kr] configuration.
|
|
Cs loses one electron to
|
gain the [Xe] configuration.
|
|
Fr loses one electron to
|
gain the [Rn] configuration.
|
We can say the same thing about
group 2A metals. That is,
|
Be loses two electrons to
|
gain the [He] configuration.
|
|
Mg loses two electrons to
|
gain the [Ne] configuration.
|
|
Ca loses two electrons to
|
gain the [Ar] configuration.
|
|
Sr loses two electrons to
|
gain the [Kr] configuration.
|
|
Ba loses two electrons to
|
gain the [Xe] configuration.
|
|
Ra loses two electrons to
|
gain the [Rn] configuration.
|
Similarly, with group 3A metals,
we can start by noting that Al loses three electrons to gain the [Ne] configuration.
(Later down in the periodic table, things get a little more complicated,
but this is a good start to our discussion!)
Much of what is said here is stated
in what is sometimes called the octet rule. That is,
an inert gas configuration is of the form, ns2
nsp6.
Such
configurations are sometime written like this:

We shall discuss this later on when
we get to Lewis structures. For now, we note that type-A elements
have this octet structure (except for H which obeys a "duet rule" which
we write simply as H: for the hydride ion).
Things become more complicated (and,
hence, more "pHun") when we look at atoms which have d-orbitals
(either occupied or empty). For instance, iron can lose either two
or three electrons to form the follow two stable ions:

We might ask why these two.
Obviously, the two 4s electrons are in the outer shell and
should go first. But, then, why just one more d-electron?
The answer here is that we are left with a 3d5
configuration. As stated in the previous chapter, a half-filled
subshell is particularly stable! That is, we have the following
configuration redrawn to accentuate Hund's rule:
 .
.
Having 5 unpaired electrons is a
peculiarly stable situation! Hence, this is what you see and get!
As we shall see shortly, ionization
energies are positive (that is, it takes energy to remove
the electron). However, that is offset by the energy gained back
from other things such as lattice energies. We shall look at these
ideas in much more detail shortly.
The ionization energy (aka
"Ionization Potential") is the energy needed to remove an electron from
an atom (which can be a neutral atom or ion in its own right). For
instance, consider the following process:

(Note that we are in the gas phase
here--this is usual for the sort of "theoretical stuff" we are handling
at the moment.)
We make note of one very important
fact:
-
Ionization energies are ALWAYS
positive.
Even though a stable compound might
form from the ionization (and this is certainly obvious for something like
Na which is never found in its free state in nature) it
still takes energy to remove the electron. We note the following
trends in any event:
-
Metals try to lose enough electrons
to reach an inert gas configuration (e.g., Na, Mg, Al, K, Ca, Sc, etc.).
-
If an inert gas configuration
is unobtainable, then half- or fully-filled subshells are what the element
"tries for" (e.g., Zn to Zn(II) and Fe to Fe(III)).
The energy needed to remove one or
more electrons to make a stable compound is usually compenstated for by
the lattice energy in a crystal or by the solvation
energy of ions. These topics will be discussed later.
Ionization energy follows periodic
trends, as do most properties of elements. For instance, here are
plotted the ionization energies of the first 92 element (H - U):
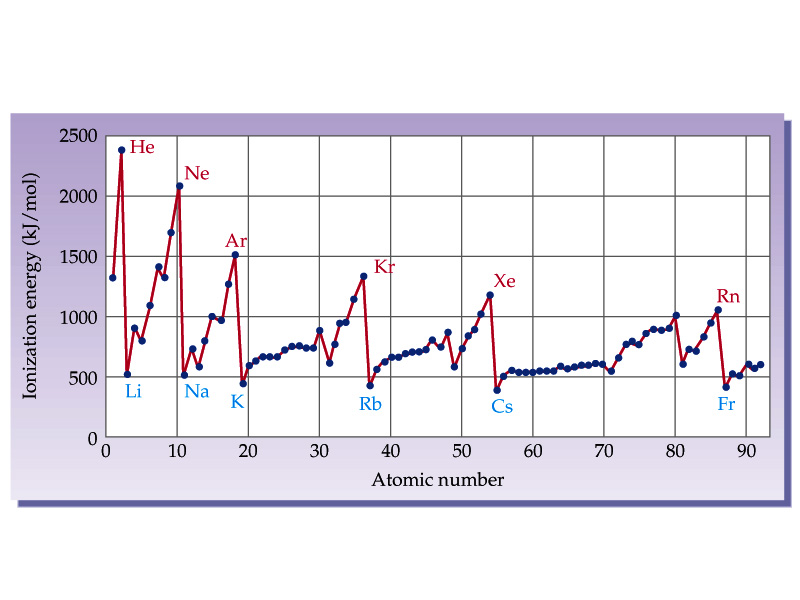 Note here that it is quite easy to
remove the first electron from elements such as Li, Na, K, Rb, Cs, and
Fr (as conveniently noted on the diagram above). It is also easy
to get the first (and also a second electon) off of the elements Be, Mg,
Ca, Sr, Ba, and Ra; these are all representative metals of groups 1A and
2A and this would be expected (getting the second electrons off of 2A metals
is not shown in the above graph).
Note here that it is quite easy to
remove the first electron from elements such as Li, Na, K, Rb, Cs, and
Fr (as conveniently noted on the diagram above). It is also easy
to get the first (and also a second electon) off of the elements Be, Mg,
Ca, Sr, Ba, and Ra; these are all representative metals of groups 1A and
2A and this would be expected (getting the second electrons off of 2A metals
is not shown in the above graph).
On the other hand, taking
electrons away from noble gases is a NONO! These are extremely stable
configurations and removing electrons is not profitable from a chemical
standpoint. Much the same can also be said for attempts to remove
electrons from halogens (group 7A) or group 6A elements (oxygen and the
chalcogens, S, Se, and Te--no one in interested in what Po thinks about
this...).
Ionization energies tend to increase
as one goes from left to right in the periodic table and to decrease as
one goes down. The above graph gave some indication of this but the
next one is even better:

There are occasional "bumps" in the
observed ionization energies. These usually occur because we are
going from s- to p- or d-electrons
in our configurations. For instance, p- and d-electrons
are more shielded than are s-electrons--so some little "burps"
might be expected. This is clearly shown for the first 20 elements
(up through Ca); here just s- vs. p-effects
are seen. To see higher effects you need to go back to the graph
of the first 92 elements (and pull out your magnifying glass)! Anyway,
here are the first 20 elements in all their "glory" as regards first ionization
energies:

Higher ionization energies
are well known for many elements. In some cases, stable ionic compounds
are formed; in other cases, these ionization energies are derived from
spectroscopic methods and are of some interest from a theoretical viewpoint.
Luckily, we need not worry too much about them other than to give them
in the following table.

Note the tremendous changes in energies
when going from the blue to the red/orange part of the table. This
dividing line is very important for metals such as Mg and Al; even for
higher elements, this large change is noted--however, elements such as
Si, P, S, and Cl form covalent compounds primarily. Ar couldn't care
less about any of this!
Many metals react (sometimes
violently) with nonmetals, the products usually being salts (except for
strong bases such as oxides). This process can be summed up into
a series of steps which is sometimes called the Born-Haber cycle.
As we shall see later and note now, in passing, this is a corollary of
the first law of thermodynamics.
As an example, we look at the formation
of sodium chloride via the reaction

The energy of this reaction is easily
measured directly and it gives off lot of heat (the word here is "exothermic"),
which is often an indication that a stable compound is being formed.
Indeed NaCl is stable--as you should well know--whereas Na and Cl2
are not found in nature in the free state. However, we know
that it takes energy to remove an electron from the Na atom and to break
the Cl-Cl bond in chlorine gas. Where does the energy come from?
The various steps which can be delineated
for this reaction are shown in the next figure.

We look at the various steps.
The first three consume energy when is then more than payed back in the
last two steps.
Step 1:
The Na is converted from
the solid to gaseous form. 107.3 kJ/mol are consumed in this process,
called sublimation.
Step 2:
The Cl-Cl bond is broken
to form gaseous Cl atoms. The energy consumed here is 122 kJ/mol
(per mole of Cl atoms produced). Note that the energy
for this process is harder to measure, as evidenced by having one less
significant figure in this number!
Step 3:
The gaseous Na atoms are
ionized at the cost of 495.8 kJ/mol (this ioization energy).
Step 4:
Finally, we start getting
energy back. The gaseous chlorine atoms become gaseous chloride ions
and receive 348.6 kJ/mol of energy (with is the electron
affinity).
Step 5:
The gaseous ions then condense
to form the solid (actually, this process is called deposition,
the opposite of sublimation). This is rather large chunk of energy,
namely 787 kJ/mol and is called the lattice energy.
Subtracting the energies of
steps 4 and 5 from the sum of steps 1, 2, and 3 gives the total reaction
energy of -411 kJ/mol of NaCl produced.
Please note that the energies of
steps 4 and 5 are formally defined as negative in the process since, with
each step, the system is losing energy. As we shall discuss later
in chapter 8, the energy change is positive for endothermic
processes (the system gains heat energy) and negative for exothermic
processes (the system loses hear energy).
Lattice energies may be caculated
rather exactly by applying Coulomb's law to the crystal lattice
(details on how this is done are left to more advanced courses).
Some typical lattice energies are tabulated below.

In the cases cited above, the calculated
lattice energy is designated as -U (negatively defined so
that we don't have to put minus signs in front of all the numbers in the
table) and the formula is

where d is the distance
of closest approach of a cation and anion, the z's are the
ionic charges, and k is a constant for the type crystal lattice
possessed by the salt. (This is sometimes called a Madelung
constant, which we now drop like a hot potato!)
Problem 6.28 (p.
238):
Which of the following
drawing is more likely to represent an ionic compound and which a covalent
compound?

(a) is clearly a crystal lattice with
ionic bonds. The even packing of this crystal particle-by-particle
should be a dead giveaway. Clearly, then, (b) represents a covalent
compound since each atom is clearly paired with just one of another type
(and, thus, we can define individual molecules--something which cannot
be done unambiguously with ionic compounds!).
Problem 6.31 (page 238):
Which of the following
spheres is likely to represent a metal and which a nonmetal? Which
sphere in the product represents a cation and which an anion?

Here we reason backwards. Clearly,
the reactants are both the same size and it is impossible to tell which
is a metal and which a nonmetal. However, we do know that anions
are larger than the atoms the come from and cations are smaller.
Hence, the metal atom is the blue one and the green atom is the nonmetal.
Problem 6.40 (p. 239):
Do ionization energies
have a positive or negative sign? Explain.
All ionization energies,
as defined, must be positive. In all
such cases energy is required to remove the electron! Hence, the
system gains energy and the number must be positive. This
actually makes sense here but will be even clearer when we get to chapter
8!
Problem 6.42 (p. 239):
Which group of elements
in the periodic table has the largest Ei1 and which has the
smallest? Explain.
We again look at the wondrous figure
imported from the textbook:

Looking at this gives the answer immediately--although
the figure should not be necessary if you understand the explanation.
We give the explanation now:
-
The most stable configurations are
those of the inert gases.
-
It takes just one electron removed
from a group 1A atom (excluding H, of course) to attain the inert gas core
configuration. Hence group 1A element have the lowers first ionization
energy.
-
Inert gases already have the most stable
configuration possible. Darned they'll be to give up that gig!
So, the answer is simple and, in any
event, the picture is certainly pretty!
Problem 6.44 (p. 239):
(a) Which has the
smaller second ionization energy, K or Ca?
Obviously, Ca. K+
has the [Ar] inert gas configuration. Ca would "like" like that,
too, and is willing to lose another electron readily to get there.
However, K+,
has already been "fulfilled" and will hold on jealously to its remaining
electrons.
(b) Which has the larger third
ionization energy, Ga or Ca?
Ca is also the "winner"
here. There is no way it would willingly surrender a third electron
to lose the happiness of being "[Ar]." However, Ga can attain "[Ar]-ness"
by losing three electrons. This, it is quite willing to do.
(And, it gets all that lattice energy, too!!!)
For both these problems, recall
the following chart:

Luckily, we won't need to talk about
this any more! (Unless you enjoy stripping electrons off of poor,
defenseless atoms!)
Problem 6.50 (p. 239):
What is the relationship
between the electron affinity of a monocation such as Na+
and the ionization energy of the neutral atom?
These are actually the same number
in magnitude. That is, the EA is just the reverse of
forming the cation. In other words, the EA of the cation is simply
the restoring of the ion to the neutral atom. We can show this with
the following simple diagram:

What we should note here is that
IE (ionization energy) and EA (electron affinity) are simply complementary
processes. The language is set in terms of neutral atoms but, overall,
the actual processes are, basically, just the changing of the number of
electrons around the nucleus.
Problem 6.58 (p. 240):
Order the following compounds
according to their expected lattice energies: LiCl, KCl, KBr, MgCl2.
Here, we note that forces are greatest
with the least distance between particles and the largest charges.
Also, lattice energies are negative but we give them in the order of their
magnitudes. This is the usual practice.
Given all that discussion, the ordering
is just
MgCl2
> LiCl > KCl > KBr.
Magnesium chloride is first because
of the +2 charge on metal cation. Then, we have anions which are
the same or bigger than chloride. So, we note that the smaller Li
cation would have a greater lattice energy than KCl and that, finally,
KCl > KBr because of the greater size of bromide.
Problem 6.62 (p. 240):
Find the lattice energy
of LiBr in Table 6.3 and calculate the energy change (in kJ/mole) for the
formation of solid LiBr from the elements. (The sublimation energy
of Li is +159.4 kJ/mol, the bond dissociation energy of Br2
is +224 kJ/mol, and the energy necessary to convert Br2(l)
to Br2(g)
is 30.9 kJ/mol.
This is much like the example given
earlier except that there is an extra step: the evaporation of liquid
bromine. We write the various steps and then sum to get the energy
change for the net reaction:
There are also some other numbers
you can get from the book. First, the IE of Li is +520.2 (p. 216)
and the EA for Br is -325 (p.226). Both these numbers are in kJ/mol.
Now we add these value for the formation of solid LiBr. The numbers
below are added or subtracted according to what you would put in the Born-Haber
cycle:
|
Process
|
Energy (kJ/mol)
|
|
Sublimation of Li
|
+159.4
|
Dissociation of Br2
(per Br atom produced)
|
+112
|
|
Vaporization of Br2
|
30.9
|
|
Ionization energy, Li
|
520.2
|
|
Electron affinity, Br
|
-325
|
|
Lattice energy, LiBr
|
-807
|
|
Total Reaction Energy:
|
-309.5
|
Note that the answer in the back
of the book is wrong (I think that they meant for you to get the EA given
the total reaction energy elsewhere--this is the way that many EA's are
obtained!) It is also possible that a couple of the numbers were
obtained off of graphs and that they forgot that they were tabulated!
In any event, this is the right answer!
![]()
![]()
![]()

 .
.



